Provided by James R. Martin, Ph.D., CMA
Professor Emeritus, University of South Florida
Learning or Experience Curve Main Page
The theory of the learning curve or experience1 curve is based on the simple idea that the time required to perform a task decreases as a worker gains experience. The basic concept is that the time, or cost, of performing a task (e.g., producing a unit of output) decreases at a constant rate as cumulative output doubles. Learning curves are useful for preparing cost estimates, bidding on special orders, setting labor standards, scheduling labor requirements, evaluating labor performance, and setting incentive wage rates.
There are two different learning curve models. The original model was developed by T. P. Wright in 1936 and is referred to as the Cumulative Average Model or Wright's Model. A second model was developed later by a team of researchers at Stanford. Their approach is referred to as the Incremental Unit Time (or Cost) Model or Crawford's Model. Simple learning curve problems are more easily introduced with Wright's model, although Crawford's model is widely used in practice. Thus, we will examine Wright's model first and Crawford's somewhat more involved approach second.
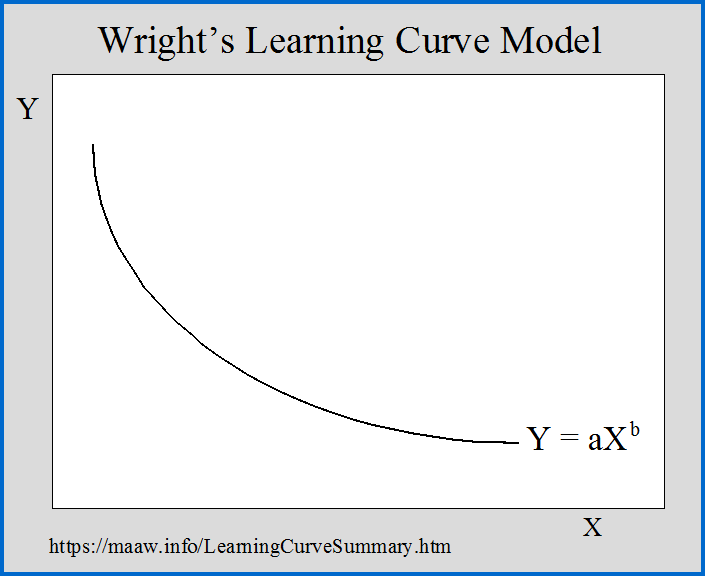
Wright's Cumulative Average Model
In Wright's Model, the learning curve function is defined as follows:
Y = aXb
where:
Y = the cumulative average time (or cost) per unit.
X = the cumulative number of units produced.
a = time (or cost) required to produce the first unit.
b = slope of the function when plotted on log-log paper.
= log of the learning rate/log of 2.

For an 80% learning curve b = log .8/log 2 = -.09691/.301 = -.32196
If the first unit required 100 hours, the equation would be:
Y = 100X-.322
The equation for cumulative total hours (or cost) is found by multiplying both sides of the cumulative average equation by X.
Since X times Xb = X1+b, the equation is:XY = aX1+b
Thus, the equation for cumulative total labor hours is,
XY = 100X1-.322 = 100X.678
An 80 percent learning curve means that the cumulative average time (and cost) will decrease by 20 percent each time output doubles. In other words, the new cumulative average for the doubled quantity will be 80% of the previous cumulative average before output is doubled. For example, assume that direct labor cost $20 per hour in the problem above. The cumulative average hours and cost as well as cumulative total hours and cost are provided below for doubled quantities 1 through 8.
| Table 1: Example of Wright's Model With an 80% Learning Curve | ||||
|
1
Cumulative Output X |
2
Cumulative Total Labor Hours XYh |
3
Cumulative Average Labor Hours Yh |
4
Cumulative Total Labor Cost XYc |
5
Cumulative Average Labor Cost Yc |
|
1
2 4 8 |
100
160 256 409.6 |
100
80 64 51.2 |
$2,000
3,200 5,120 8,192 |
$2,000
1,600 1,280 1,024 |
Note that the cumulative average columns, 3 and 5 decrease by 20% as output is doubled, or the new cumulative average is 80% of the previous cumulative average. The cumulative total columns 2 and 4 increase at a rate equal to twice the learning rate, or 160% in this case. Since these rates of change remain constant, tables for doubled quantities can be developed easily. However, for quantities in between the doubled quantities, the equations are required. For example, assume the firm has produced eight units as indicated in the table. How much will it cost to produce ten additional units? Any of the equations for Yh, Yc, XYh or XYc may be used to solve the problem. However, working with the equation for cumulative total cost is the fastest way to obtain the solution. The answer is found by subtracting the cost of the first 8 from the cost of producing the first 18. Using the equation for cumulative total cost generates the answer in two steps as follows:
Cost of first 18 = XYc
= $2,000(18).678 = $14,194
Less cost of first
8 -8,192
Cost of 10 additional
units
$6,002
Thus, producing 10 additional units will require approximately $6,002 of additional direct labor cost.
Crawford's Incremental Unit Time (or Cost) Model
The equation used in Crawford's model is as follows:
Y = aKb
where: Y = the incremental unit time (or cost) of the lot midpoint unit.X (i.e., the cumulative number of units produced) can be used in the equation instead of K to find the unit cost of any particular unit, but determining the unit cost of the last unit produced is not useful in determining the cost of a batch of units. The unit cost of each unit in the batch would have to be determined separately. This is obviously not a practical way to solve for the cost of a batch that may involve hundreds, or even thousands of units. A practical approach involves calculating the midpoint of the lot. The unit cost of the midpoint unit is the average unit cost for the lot. Thus, the cost of the lot is found by calculating the cost of the midpoint unit and then multiplying by the number of units in the lot.
Since the relationships are non linear, the algebraic midpoint requires solving the following equation:
K = [L(1+b)/(N21+b - N11+b)]-1/bAn example of an 80 percent learning curve based on Crawford's unit time (or cost) model can be developed in much the same way we developed Table 1, except that the unit values for the doubled quantities decrease by 20% rather than the cumulative average quantities.
| Table 2: Example of Crawford's Model with an 80% Learning Curve | ||||
|
1
Cumulative Output X |
2
Incremental Unit Labor Hours Yh | 3
Cumulative Total Labor Hours Kh (Yh) |
4
Incremental Unit Labor Cost Yc |
5
Cumulative Total Labor Cost Kc(Yc) |
|
1
2 4 8 |
100
80 64 51.2 |
100
180 314.2 534.6 |
$2,000
1,600 6,284 1,024 |
$2,000
3,600 6,284 10,692 |
Notice from Table 2 that the unit labor hours (column 2) and unit labor cost (column 4) decrease by 20% each time the cumulative output is doubled. However, the cumulative total labor hours (column 3) and cumulative total labor cost (column 5) increase by a variable rate. This means that columns 3 and 5 are much more difficult to develop. It also means that the cumulative total hours and cost generated by the two models are not compatible when based on the same learning rate. For example, compare column 2 in Table 1 with column 3 in Table 2. The cumulative total hours for 8 units is 409.6 based on Wright's model and 534.6 based on Crawford's model. Another difference is that the cumulative average hours and cost decrease by a variable rate in Crawford's model. This does not present a problem when using Crawford's model because the cumulative averages are not required for predicting cost.
To illustrate the use of the algebraic midpoint equation and Crawford's approach, assume that the firm in the example above has produced 2 units and wants to determine the cost of producing 4 additional units. One way to find the answer is to calculate the unit cost for each unit 3 through 6 and then sum those values. That works reasonably well for a lot of 4 units, but would not be a practical way to determine the cost of 40, 400, or 4,000 additional units. The midpoint of the lot is:
K = [L(1+b)/(N21+b - N11+b)]-1/b = [4(.678)/(6.5.678 - 2.5.678)]1/.322
= [2.712/(3.55758 - 1.86124)]3.10559 = 4.2938
The cost of the mid point unit is:
Yc = $2,000(4.29385)-.322 = $1,250.99
and the total cost for the lot of 4 = 4(1,250.99) = $5,005
An alternative is to use the equation for hours as follows:
Yh = 100(4.29385)-.322 = 62.5494 hours
Then the total cost for the lot of 4 is 4(62.5494)($20) = $5,004.
Finding the Learning Rate When Doubled Quantities are not available
The equations provided above show how to use the learning curve to predict the time and cost of a specific quantity of units assuming that we know the learning rate. An important question, ignored to this point, is how do we find the learning rate in the first place? If we have data for two lots of units we can find the learning rate by using simultaneous equations. For example, assume two lots have been produced, one lot contained 2 units and a second lot contained 4 more units.
| Lot | Number of Units in the Lot |
Cumulative Units |
Labor Hours for the Lot |
Cumulative Labor Hours |
| 1 2 |
2 4 |
2 6 |
72 111 |
72 183 |
We can solve for the learning rate using either Wrights model or Crawford's model, but the procedures and learning rates are different.
Using Wright's Model to find the Learning Rate:
The equations for the 2 lots are:
XY = aX1+b
72 = a(2)1+b
183 = a(6)1+b
Converting these to the log forms we have:
log 72 = log a + (1 + b)(log 2)
log 183 = log a + (1 + b)(log 6)
Calculating the log values indicated we have:
1.8575 = log a + (1 + b)(.301)
2.2625 = log a + (1 + b)(.7782)
1.8575 = log a + .301 + .301b
2.2625 = log a + .7782 + .7782b
Subtracting the first equation from the second equation provides the following equation which can easily be solved for b.
.405 = .4772 + .4772b
b = -.151299
Substituting b into either of the original equations, a = 40.
Then the learning rate is found by using the equation for b, i.e.,
b = log of learning rate / log of 2
-.151 = Log of learning rate / .301
log of learning rate = -.151(.301) = -.04545
The learning rate = the antilog = 10-.04545 = .90
Thus, the equation for cumulative average hours is:
Y = 40X-.151
and the equation for cumulative total hours is:
XY = 40X.849
Using Crawford's Model to find the Learning Rate:
To find the learning rate using Crawford's model, we must find the algebraic midpoint for each lot which is needed in the equations that must be solved simultaneously. We can't use the formula for K because it includes the value of b which is unknown. Thus, we must use the alternative midpoint formulas described by Liao [see p. 309].
The midpoint of the first lot is:
A = [(L + 1)/3] + .5 = (2+1)/3 + .5 = 1.5
The midpoint of subsequent lots is:
A = (L/2) + total units in all preceding lots = 4/2 + 2 = 4
After finding approximate midpoints we can develop two equations, one for each lot as follows:
Find the average hours for the midpoint units:
72/2 = 36 for the midpoint in lot 1.
(183 - 72)/4 = 27.75 for the midpoint in lot 2.
Then the equations are:
36 = a(1.5)b
27.75 = a(4)b
Converting to the log forms:
log 36 = log a + b(log 1.5)
log 27.75 = log a + b(log 4)
1.5563 = log a + b(.17609)
1.44326 = log a + b(.603)
Changing the signs in equation 2 and then adding the two equations provides:
.11304 = -.4259b
b = - .2654
Then a is determined:
36 = a(1.5)-.2654
a = 40.09
The equation for incremental unit time is:
Y = 40.09X-.2654
The learning rate is found by using the equation for b as indicated above in the example for Wright's model.
b = log of learning rate/log of 2
-.2654 = log of learning rate/.301
Log of learning rate = (.301)(-.2654) = .079885
The learning rate = antilog .079885 = .83198.
Comparing the two learning rates we have .90 for Wright's model and .832 for Crawford's model. This reinforces the fact that the two models are not compatible when the same learning rate is used. In other words, the same set of data will always generate two different learning rates under the two separate models because unit time and cumulative average time do not decrease at the same rate. The best model is the one that generates time and cost estimates that are closest to the actual results.
Learning curves range from around 70% to 100%. A learning curve below 70% is rare. A 100% learning curve indicates no learning at all. On the other hand, a 50% learning curve would indicate that no additional time or cost would be required for additional units beyond the first unit, since the cumulative average time, (in Wright's model) or the incremental unit time (in Crawford's model) would decrease by 50% each time output doubled. This means that the cumulative total time would not increase because it would equal 100% of the previous cumulative total time.
______________________________________________
1 The term experience curve is more of a macro concept, while the term learning curve is a micro concept. The term experience curve relates to the total production, or the total output of any function such as manufacturing, marketing, or distribution. The development of experience curves is attributed to the work of Bruce Henderson of the Boston Consulting Group around 1960.
Liao,S. S. 1988. The learning curve: Wright's model vs. Crawford's model. Issues in Accounting Education (Fall): 302-315.
Morse, W. J. 1972. Reporting production costs that follow the learning curve phenomenon. The Accounting Review (October): 761-773.
* For more information on the learning curve models, see the Learning Curve Bibliography.